Finken-Minis Finken-Minis Mathe 3/4
22,10€
inkl. MwSt. zzgl. Versandkosten
BNr.: 1553
Sach- und Knobelaufgaben
ab 3. Schuljahr
Christiane Peters
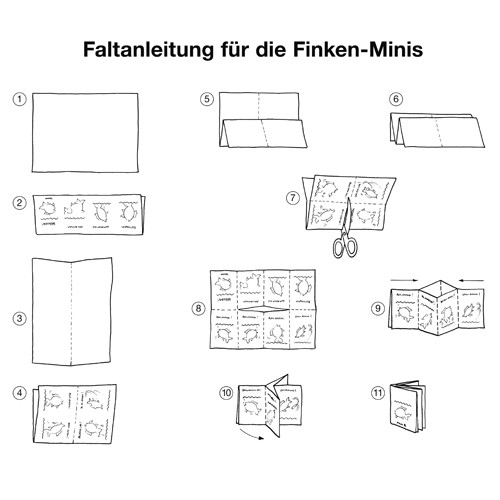
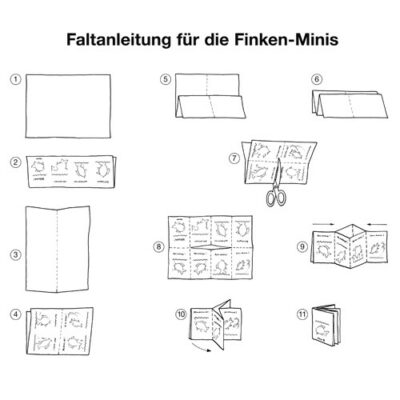
Durch einfaches Falten und einen Schnitt entsteht ein Büchlein, das die Kinder vor spannende und herausfordernde mathematische Aufgaben stellt. Jedes Büchlein erzählt eine lebendige Geschichte aus dem Lebensumfeld der Kinder, die mit verschiedenen mathematischen Problemstellungen verknüpft ist. Diese gilt es durch Probieren, logisches Denken, Rechnen oder durch ganz individuelle Strategien zu lösen.
Die Lösungen werden direkt in das Büchlein eingetragen. Die vollständig bearbeiteten Büchlein können dann in einer Sammelbox aufbewahrt werden (eine Faltvorlage ist enthalten), sodass die kleinen Mathe-Detektive immer wieder stolz darauf zugreifen können.
Zu jedem Büchlein sind die Lösungen beigefügt.
Konzept
Die Finken-Minis sind eine höchst motivierende Alternative zum herkömmlichen Arbeitsblatt. Der Ehrgeiz, ein Büchlein vollständig zu lösen, bietet Schülern den nötigen Anreiz, sich auch an anspruchsvolle Aufgaben heranzuwagen. Daher ist dieses Format ideal, um Kinder für Sach- und Knobelaufgaben zu interessieren und ihren mathematischen Eifer zu wecken.
Der Zahlenraum wurde bei den Aufgabenstellungen bewusst niedrig gehalten, um im Sinne einer natürlichen Differenzierung allen Kindern einen Lösungsansatz zu eröffnen. So werden leistungsschwächere Schüler durch Probieren zu einer Lösung gelangen, während leistungsstärkere Kinder auch mathematisch-logische Lösungsansätze entwickeln werden.
Bestimmte Aufgabenformate tauchen in wechselnden Zusammenhängen immer wieder auf, sodass die Kinder ihre Lösungswege kontinuierlich erproben und verfeinern können.
Die Büchlein sind ideal für die Wochenplan- und Freiarbeit, bieten aber auch für Knobelstunden und Mathekonferenzen ein vielfältiges und reizvolles Aufgabenangebot.
Zu jedem Büchlein sind die Lösungen beigefügt. Diese Lösungsseiten können sowohl von der Lehrkraft als auch von den Schülern zur schnellen Ergebniskontrolle genutzt werden.
Kompetenzen und Förderschwerpunkte
- mit Größen in Sachsituationen umgehen
- mathematische Kenntnisse, Fertigkeiten und Fähigkeiten bei der Bearbeitung problemhaltiger Aufgaben anwenden
- Lösungsstrategien entwickeln und nutzen
- für das Bearbeiten mathematischer Probleme geeignete Darstellungen entwickeln, auswählen und nutzen
- eigene Vorgehensweisen beschreiben, Lösungswege anderer verstehen und gemeinsam darüber reflektieren
| Schulstufe / Alter | 3. Schuljahr, 4. Schuljahr |
|---|---|
| Produkttyp | Kopiervorlagen – Hefte |
| Serie | FinkenMinis |
| Fach | Mathematik |
| Bestandteile | Kopiervorlagen für 28 Mini-Bücher mit Sach- und Knobelaufgaben |
| Kompetenzen | mit Größen in Sachsituationen umgehen |
Ähnliche Produkte
Artikel-Nr.: 1694 (Set aus 1691 & 1692) Kopfrechenkarteien Klasse 1 und 2 Karin Scheuermann, Meike Weiss
inkl. MwSt.
zzgl. Versandkosten
Artikel-Nr.: 1691 Kopfrechenkartei ab 1. Schuljahr Karin Scheuermann, Meike Weiss
inkl. MwSt.
zzgl. Versandkosten
Artikel-Nr.: 3729 Mathe für Asse LOGICO-Set MAXIMO ab Klasse 3 von Ellen Basten, Jessica Drath, Rebekka Scholz
inkl. MwSt.
zzgl. Versandkosten
Artikel-Nr.: 3601 Rahmen mit 18 Knöpfen, dunkelrot ab 3. Schuljahr
inkl. MwSt.
zzgl. Versandkosten
Artikel-Nr.: 1695 Pfiffige Kopfrechenkartei mit Rechentaschen 3. & 4. Schuljahr von Karin Scheuermann, Meike Weiss
inkl. MwSt.
zzgl. Versandkosten
Artikel-Nr.: 1692 Kopfrechenkartei ab 2. Schuljahr Karin Scheuermann, Meike Weiss
inkl. MwSt.
zzgl. Versandkosten
Artikel-Nr.: 3015 Stufe 4: Zahlenraum bis 1 Million ab 4. Schuljahr Marco Bettner, Erik Dinges (Hrsg.), Silke Hofmann, Silke Petersen, Andrea Schuberth
inkl. MwSt.
zzgl. Versandkosten
Artikel-Nr.: 3738 LOGICO-Set MAXIMO ab Klasse 3 von Susanne Kortmann
inkl. MwSt.
zzgl. Versandkosten